Les enseignants des écoles de Saint Pierre en Faucigny, ont travaillé, autour de 4 axes de la résolution de problèmes, dans le cadre du Plan Mathématiques 2022_2023 et de la formation en constellations :
- Enseigner la schématisation
- Construire des traces écrites individuelles et collectives
- Ecrire des énoncés de problèmes en lien avec une typologie travaillée en classe
- Comprendre l'importance du choix des données numériques sur les stratégies des élèves pour résoudre des problèmes de proportionnalité en C3.
3. Ecrire des énoncés de problèmes en lien avec une typologie travaillée en classe :
- Comment aider les élèves à produire des énoncés de problèmes ? il s’agit grâce à une situation d'écriture, d’amener les élèves à développer leur capacité à mobiliser, à transférer les savoirs construits dans d’autres contextes. En inventant un énoncé de problèmes proche d'une situation de référence travaillée en classe, l'enseignant a un retour sur la compréhension de la structure interne du problème par l'élève. En s'engageant dans la création d'un énoncé de problème, l'élève explicite une démarche et argumente son raisonnement. Un projet d'écriture d'énoncés de problèmes nécessite une compréhension et une analyse fine de la structure interne d'un problème.
- Voici les structures qui ont été préalablement travaillées en classe pour les problèmes additifs :
- Une structure de réunion de deux quantités dans laquelle on cherche soit le tout soit une partie ; de comparaison dans laquelle on cherche soit l’écart, soit une des deux quantités ; de transformation dans laquelle on cherche soit la valeur du gain ou de la perte, soit la transformation soit encore la situation initiale avant la transformation.
- Les situations qui ont été travaillées en classe pour les problèmes multiplicatifs :
- Une situation dans laquelle on cherche le nombre total d’éléments ; une situation de partage dans laquelle on cherche la valeur d’une part ou le nombre de parts ; une situation de proportionnalité.
L'élève est éloigné en premier lieu des données numériques et concentre son attention sur la cohérence de la structure (plutôt que sur les éléments narratifs de l'histoire qui tiennent du thème), des informations à fournir, de la question à poser et à laquelle il est possible de répondre grâce aux mêmes informations. C'est une étape dans la compréhension des énoncés de problèmes.
Faire inventer des problèmes de la typologie travaillée :
- Afin de ramener les élèves sur la recherche mathématique, les enseignants ont choisi de prendre en charge une partie de l’énoncé en étant vigilants quant au contexte et au lexique :
- Donner déjà 2 nombres, par exemple, 8 et 3 ou 12 et 17. Parfois, les prénoms des personnes dans les énoncés de problèmes ont été déjà donnés.
- Partir du schéma en barre.
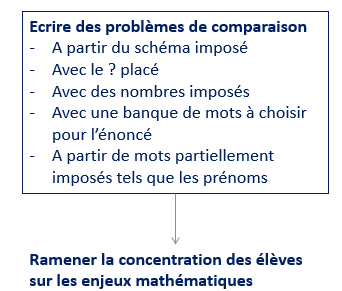
- On peut demander aux élèves de créer tout l’énoncé, les objectifs sont différents. En laissant les élèves libres d'inventer leurs situations, ils montrent ce qu'ils ont intégré. Lors de travaux de groupes, les élèves se confrontent aussi à l’argumentation pour choisir les propositions. On met en évidence des difficultés de syntaxe et de réciprocités dans les formulations : "combien tu en as de plus, combien j’en ai de moins", "combien il faudrait pour en avoir autant que".


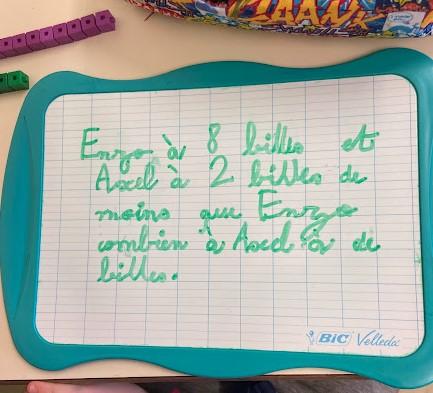

La production d'énoncés de problèmes guide les élèves vers la compréhension de la structure interne du problème quelles que soient les données numériques et les éléments thématiques (histoires de poules, de cartes, de bus ...).
- Point de vigilance : Au préalable, on aura bien appris à schématiser et on aura valorisé la mise en place progressive d’un schéma codifié (commun à la classe, le cycle, l’école). Bien inciter les élèves à verbaliser les ressemblances et les différences entre les problèmes. Les éléments de surface changent : noms, objets, nombres - la structure interne est identique : ce qui est connu, ce qui est inconnu, ce que l'on cherche. L'objectif est que la structure du problème fonctionne, les corrections orthographiques feront l'objet d'une autre séance pour mise au propre et partage entre élèves.
